En la actualidad para obtener el valor de una razón trigonométrica a partir de un ángulo dado, simplemente se utiliza una calculadora en la cual se introduce el valor del ángulo dado y se evalúa en la relación trigonométrica requerida. Los valores de estas razones también se pueden obtener utilizando triángulos rectángulos, cuyos ángulos serán a los que se les quiere encontrar sus razones trigonométricas. En ocasiones este método es muy engorroso, ya que para crear los triángulos se deben realizar bastantes operaciones. Sin embargo, existen ángulos en los que es muy fácil; a estos ángulos se les conoce como ángulos notables.
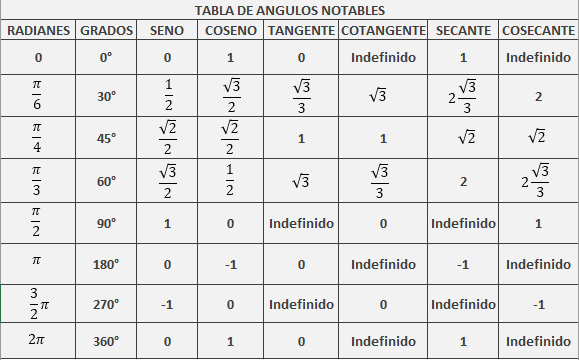
En las matemáticas y específicamente en la Trigonometría, la palabra notable se utiliza para referirnos a procesos o valores que están bien definidos o muy comunes, y por ende, se reconocen y memorizan fácilmente. En este sentido, los ángulos notables son aquellos que tienen valores que aparecen muy seguido en la vida cotidiana. Estos ángulos son los de 30°, 45° y 60° y, en segundo lugar, los ángulos de 0°, 90°, 180°, 270° y 360°. Estos últimos, aunque no están definidos como notables, también son muy comunes.
ACTIVIDAD PRÁCTICA
1) 
2) 
3) 
4) 
5) 
No hay comentarios:
Publicar un comentario